October 28, 2019 Graph
안녕하세요 오늘 리뷰할 논문은 Graph Convolutional Networks 입니다. GCN은 그래프 구조에서 사용하는 Graph Neural Network의 일종으로 2016년에 나온 논문이지만 convolution filter의 특징을 graph에 적용했다는 점에서 Graph 기반 이론의 시작에 적합하다고 생각합니다. 그럼 논문 요약 진행하겠습니다. 논문의 내용 및 사진 출처는 GCN_github 및 GCN_towardsdatascience 를 참고하였습니다.
들어가며
딥러닝에서 대표적인 Task는 이미지 분야일 것입니다. Convolution filter와 함께 이미지의 분류에서 가공할 성장을 보이면서 딥러닝은 새롭게 주목받기 시작했습니다. 그러나 Convolution filter는 이미지와 같이 고정된 그리드 형태의 이미지에 효과적이라는 한계를 갖습니다. 오늘 소개하는 GCN은 그래프에서 convolution filter와 같은 효과를 통해 그리드 형태가 아닌 데이터에서도 효과적으로 feature extraction 및 학습이 가능하도록 접근했습니다.
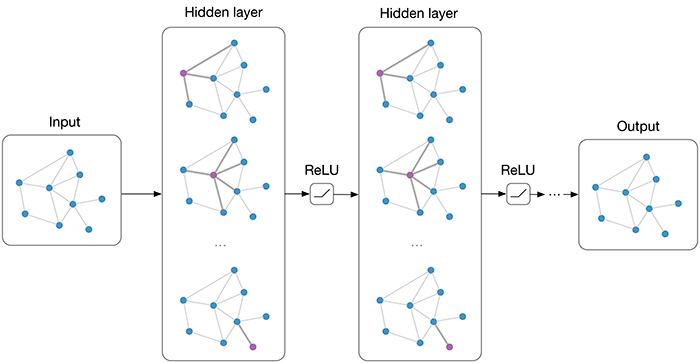
다층 GCN의 예시
위의 그림은 2개의 은닉층으로 구성된 GCN입니다. 각 은닉층 및 활성함수를 지나 학습이 진행된다는 점에서 기존의 MLP와 크게 다르지 않습니다. 중요한건 각 은닉층이 갖게 되는 구조입니다.
Definitions
위의 예시와 같이 GCN은 간단한 구조를 갖고 있습니다. N개의 노드와 E개의 엣지로 구성된 그래프 graph(N,E)가 있을 때, 각 노드를 d차원으로 embedding한다면 \(n \times d\) 차원의 input값을 구할 수 있을 것입니다. GNN은 추가로 엣지 정보를 반영한 인접행렬을 사용합니다.
- Graph(N,E)
- input X : \(n \times d\)
- adjency matrix A : \(n \times n\)
이후 X와 A 정보를 은닉층에 사용하여 그 다음 은닉층으로 전달합니다. \(H^0 = X\) 라 하면 l번째 은닉층에 대한 값은 은닉층 함수 f를 사용하여 다음과 같이 정의할 수 있습니다.
\[H^l = f( H^{l-1}, A)\]각 은닉층 함수 f를 지나 input data에서부터 예측값까지 학습이 진행됩니다. 간단한 예시는 아래와 같습니다.
\[f( H^{l}, A) = \sigma (AH^{l}W^{l})\]즉, GCN은 MLP처럼 가중치를 구하는 모델이지만 그 과정에서 그래프 구조에서 얻을 수 있는 정보를 반영하는 방식입니다.
Practical Implementation
- 자기 자신에 대한 엣지 추가 (adding self-loops)
실제 적용을 위해서 노드 간의 관계 정보를 반영하는 인접 행렬에 self-loop을 추가해줘야 합니다. 즉 인접 행렬 A에 항등 행렬 I를 더해주는 접근법을 통해서 하나의 노드에 대한 representation을 구할때 다른 노드와의 관계와 함께 자기 자신의 embedding 까지 고려하도록 만들어줍니다.
- normalization 적용
강건한 representation을 구하기 위해 normalization을 적용해야 합니다. 노드간의 관계를 반영해야 하다보니 연결된 엣지의 개수, 즉 degree가 높은 노드와 아닌 노드와의 차이가 심할 수 있습니다. 이러한 차이를 줄이기 위해서 normalization을 통해서 데이터를 scaling해주는 작업을 거칩니다. 그래프 이론에서 인접행렬의 normalization은 degree의 값을 갖는 대각행렬의 역행렬을 인접행렬에 곱해주어서 계산합니다.
모델 적용
논문에서는 준지도 학습에 GCN을 적용한 결과를 보여줍니다. 아래 그림과 같이 GCN을 사용하여서 그래프 데이터로부터 잘 구분되는 embedding을 구했다는 것을 알 수 있습니다.
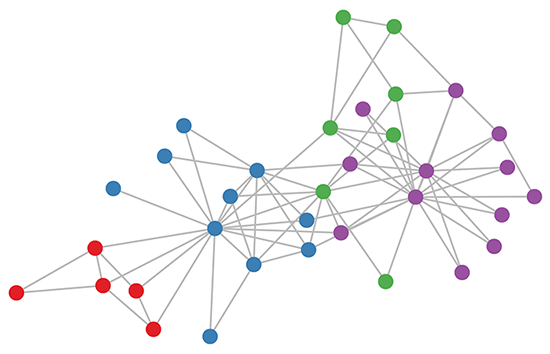
Zachary's Karate Club Dataset
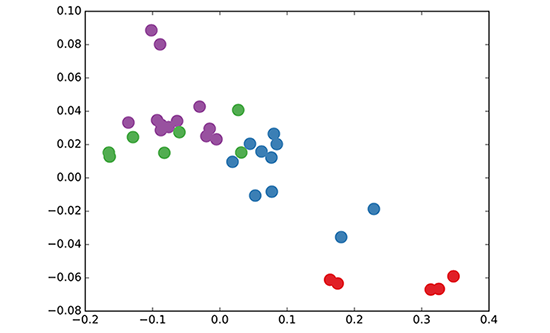
각 노드에 대한 GCN embedding 결과
결론
GCN은 GNN의 기초적인 접근법으로 그래프 구조에서도 convolution filter와 같이 강건한 특징 파악을 가능하게 해주는 구조입니다. 이를 이어서 graphSAGE, GAT 와 같은 논문들이 제안되었는데 다음에는 GAT를 다루도록 하겠습니다.