안녕하세요 오늘 리뷰할 논문은 Graph Attention Networks 입니다. Attention은 딥러닝에서 요인 분석 및 성능 향상을 위해 쓰이는 대표적인 기법입니다. GAN 또한 Attention을 사용해서 GNN에서의 성능 향상을 추구합니다. 그럼 논문 요약 진행하겠습니다. 논문의 내용 및 사진 출처는 Attention , GAT_github 및 GAT논문 을 참고하였습니다.

들어가며

GAT의 가장 핵심적인 아이디어는 각 노드에 대해 multi-head attention을 적용했다는 점입니다. Multi-head attention이란 대표적인 attention 모델인 Transformer에서 사용한 기법으로 아래 그림과 같이 전체 차원을 나누어서 linear projection을 여러번 수행하여 더 풍부한 representation을 얻는 기법입니다.

Multi-head Attention

아래의 그림은 multi-head attention이 적용된 노드1의 모습을 보여줍니다. 서로 다른 형태와 색의 화살표가 multi-head를 통해 구하는 attetnion값을 의미합니다.

GAT Layer

---

Architecture

각 노드의 차원이 F인 N개의 노드를 입력값으로 한다면 출력값으로 $F^{‘}$ 인 차원의 N개의 노드를 얻을 수 있습니다.

\[h = {h_1, h_2, ..., h_N}, h_i \in R^F\] \[h^{'} = {h^{'}_1, h^{'}_2, ..., h^{'}_N}, h_i \in R^{F^{'}}\]

위와 같이 노드의 입력 차원으로부터 고차원의 representation을 얻기 위해 linear transformation을 행해야 합니다. GAT에서는 고차원의 representation을 얻기 위한 방법으로 가중치 matrix $W$ 를 사용하며 self-attention을 각 노드에 적용합니다. Self-attention을 통해 attention coefficient를 구할 수 있는 데 이는 i번째 노드에 대해 j번째 노드의 특징의 중요성을 의미합니다.

</a>

attention coefficients

그래프 구조를 유지하기 위해서 서로 간의 연결되어 있는 이웃 노드의 coefficient만을 계산하며 노드 i에 대한 j번째 노드의 특징 계산 과정에서 Softmax를 활용한 normalization을 실시합니다.

</a>

Softmax function

본 논문에서는 한개의 feed-forward 네트워크가 되며 activation fuction으로 비선형 LeakyReLU를 적용했습니다. 최종적으로 아래와 같이 표현됩니다.

</a>

final coefficients mechanism

아래는 위의 과정을 도식화한 그림입니다. 최종적으로 softmax를 통해 attention coefficient를 구하게 됩니다.

</a>

attention mechanism

앞선 과정에서 구한 attention coefficient 값을 linear combination에 적용하여 output feature를 뽑아내게 됩니다.

</a>

linear combination using attention coefficients

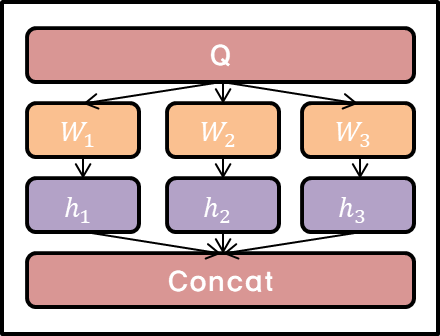
그 과정에서 multi-head attention 기법을 적용하는데, 위에서 언급한 바와 같이 K개 만큼의 독립적인 차원으로 나누어 계산을 진행한 후 최종적으로 concat하여 원래의 차원과 동일하게 만들어줍니다. 이 과정을 통해서 더욱 안정되고 풍부한 representation을 구할 수 있습니다.

</a>

multi-head attention

네트워크의 마지막 층에서는 concatenate하지 않고 각 독립된 값의 평균을 취해서 입력값으로 사용합니다.

</a>

Averaging multi-head representation

---

모델 적용

GAT를 통해 구한 결과를 t-SNE로 시각화한 결과는 아래와 같습니다. attention coefficient 값에 따른 시각화 결과 Cora 데이터셋으로부터 데이터의 특징에 따른 적절한 representation을 얻을 수 있엄음을 확인할 수 있습니다. 추가적으로 논문에서는 GCN 또는 GraphSAGE 방법론보다 더 나은 성능을 보임을 보여주고 있습니다.

t-SNE + Attention coefficients on Cora

---

결론

GAT방법론은 Attention mechanism이 딥러닝에서 각광받으면서 GNN에도 적용되어 성능 향상을 가져온 방법입니다. GCN이 갖고 있는 고정된 filter의 한계를 뛰어넘으면서 Attention mechanism의 장점까지 활용할 수 있기에 많은 활용 가능성을 갖고 있습니다. GAT는 제가 공부하고 있는 Visual Question Answering 분야에서도 많이 활용되며 성능을 향상시키는 좋은 기법이며 저 또한 GAT방법론으로부터 더 나은 방법론을 개발하기 위해 연구하고 있습니다.

---